We need to find the single most asymmetric spiral because the fundamental concept we seek to model is The Primary Distinction, the most basic bifurcation at the "start" of creation. If we are sufficiently abstract, our model will be the same regardless of whether we seek the Big-Bang, The Creator or Both. The primary distinction has been formally conceptualized (topologically) by Spencer-Brown as the mark of distinction between inside and outside. We seek to model and thus better understand the primary distinction because of its extraordinary elegance and because of the extraordinary applicability of its fundamental generative properties.

We have chosen to model the primary distinction between inside and outside both directly and by means of other dichotomies of similar intensity. Thus we see a seed inside and a fruit outside, a sun inside and a firmament outside, our personal consciousness inside and the consensus world outside. These all refer to things. When we examine abstract models that express the primary distinction with extreme elegance, utter accuracy and maximum contrast we find that the distinction between symmetry and asymmetry is the best candidate.

Each requires the other for its definition. When each is expressed in the extreme, together they can model the most extreme, the most primary, distinction. But, we need models that do more than just include features that can represent symmetry and asymmetry. In order to model the primary distinction we must (to the extent possible) have models of perfect symmetry with no other elements and models of perfect asymmetry with no other elements. To the extent that our choice of models includes gratuitous features, their clarity would be diluted and they would not be as close to modeling the primary distinction as they could be if they did not include features that diluted their elegance.

How are we to test if our models are as elegant and unambiguous as is possible? Since they are intended to be as nearly perfectly complementary opposites as is possible, we can test them by comparing them. Unless we have a sense of asymmetry we cannot notice when something is symmetrical; unless we have a sense of symmetry we cannot notice when something is asymmetrical. ...And we should be able to find corresponding features between our model of symmetry and our model of asymmetry because the parts of our models should be as complementary as the models themselves. Plato refers to the same and the different (although most scholars believe these are aspects of astronomical cycles), while the kabbalists discuss the Urim (Lights) and Thummin (Perfections) -- which may also allude to asymmetry and symmetry. However it is that we choose to model the same, if we are seeking a model of highest contrast for the first distinction, we should model the different, feature by feature, in a corresponding, but complementary or reciprocal way. Thus no matter how we examine each model they will always appear to be complementary or reciprocal - they will always stand in high contrast -- which is exactly what we want in a model that demonstrates nothing but the high contrast of the primary distinction.

Thus our model of unity will consist of two complementary components, one utterly symmetrical and the other utterly asymmetrical. The ideal symmetrical component for our model is relatively simple to find. We know that the five Platonic solids most elegantly express spatial symmetry in 3-dimensions - and nothing else. For our purposes, the first, the simplest, the most elegant Platonic solid is the tetrahedron. It will be our vessel, the logical frame that quantizes and counts. It represents the structure and scaffolding of our model of symmetry. Each of its parts and components has the same-symmetric relationship with all the others in the same sense. Minimally, a tetrahedron is defined when 4-equal spheres are in closest mutual contact. Their centers form the 4-corners of the tetrahedron. The 6-lines that connect their centers form the edges of the tetrahedron which frame the 4-perfect triangular faces of the tetrahedron. There is only one way to arrange the 4-spheres because all permutations are indistinguishable. No feature is favored, each is in the same relationship to all the others as is every other similar feature, no part is gratuitous, all parts are accounted for, no fewer could be used. Therefore, it is not hard to justify the use of a regular tetrahedron to model perfect symmetry in 3-dimensions. (It should be noted however, that the use of any of the other four platonic solids could also be easily justified by the nearly all of the same arguments. The only feature that recommends the tetrahedron over the others is that it exhibits one added symmetry. The tetrahedron is uniquely self-dual. However, if we needed or chose to include 5-fold symmetry, we might chose to sacrifice the self-dual symmetry of the tetrahedron in favor of the 5-fold symmetry of the icosahedron. No matter how unambiguous the pure mathematical choices seem to be, we will always have to weigh one feature against another depending on what we believe to be more important in any particular application. Our knowledge and our esthetic sense underlies our choices of models and metaphors. Pure mathematics does not make metaphor, we do.)

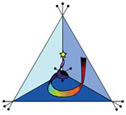
The Kabbalists suggest that "Unity exists when a flame is wedded to a coal," or when a light is in its proper vessel. If our utterly symmetrical tetrahedron represents the coal/tent/vessel, then an utterly asymmetrical spiral vortex with corresponding, but inverse, features can represent its complementary flame. Together the tetrahedron and vortex can represent a geometric metaphor of the "Light in the Meeting Tent," the "Urim and Thummin," and the "same and the different."

What form should the spiral that generates our vortex-flame take? It should be the most asymmetrical spiral. That is required of a fitting complement to the most symmetrical tetrahedron. If the flame were not as utterly asymmetrical as the tetrahedron is utterly symmetrical, then we would not have a model of highest contrast and we would not have a very good model of the primary distinction. The best model we can make requires us to pick a most symmetrical form (or possibly a most omni-symmetrical from such as a sphere) and then to find a most asymmetrical complement to contrast it with. The greater the contrast between the form we pick to represent the symmetrical component and the form we pick to represent the asymmetrical component, the more closely we can model the primary distinction.

How can we create or find a spiral that is most asymmetrical? What do we mean by asymmetrical when referring to spirals? Aren't all spirals asymmetrical? Yes, but sometimes only to the extent that they exhibit handedness. Spirals can open clockwise or counter-clockwise. Thus any single spiral without its mirror-twin must be asymmetrical in this respect. (Some mathematically defined spirals are intrinsically symmetrical in this regard explicitly because they come with their mirror images.) The simple understanding of symmetry entails visualizing a mirror image or a pattern that repeats by rotation. But the concept of symmetry includes patterns that repeat by translation and scaling as well. By these standards, some spirals are more asymmetrical than others and some are highly asymmetrical but include features that do not relate to asymmetry or symmetry.

For example, Archimedes' spiral is formed by a coil that expands radially winding on winding. Every section is the same if you allow for an expanding scale. The Archimedean spiral is too regular. Except for its natural handedness, it is not very asymmetrical. It has a simple symmetry inherent in its design.

Likewise, all logarithmic spirals (including the famous Golden Mean or Fibonacci series spiral) are always the same shape no matter where you examine them. Except for scale every section of a logarithmic spiral is identical to every other section. This self-similarity is their hallmark and a defining feature. It is retained even when you pull on the ends of the naturally 2-dimensional spiral and stretch it into a vortex-like spring in 3-dimensions. All logarithmic spirals are highly symmetrical with respect to scaling and rotation.

We need a spiral that is the most asymmetrical. Perhaps we could construct one. How could we do this? It is not difficult to devise a strategy. If we do everything the opposite (with regard to symmetry properties) of what we did to construct the most symmetrical solid, the tetrahedron, that could suggest some of the qualities of the most asymmetric spiral.

The most fundamental aspect of the structure of a tetrahedron that makes it so symmetrical is that it consists of a maximum of components that are all alike in a minimal structure. This is what we mean by high symmetry: as much of the same as possible in as little of the different. So if we would like to find its complement, we should seek a minimum set of the same components that are as different as possible. (There is a self-referential aspect built into this. After all we are here seeking to construct a minimal model of the distinction between two components, inside and outside, that are as different as possible - based on the distinction between the same two components.)

The minimum number of components possible is two -- and they must be very different from each other (just as inside and outside). What are the two most basic and most different sorts of curves (that we will need to construct our spiral)? What is the primary distinction possible for a line? A line can either be straight or it can be curved. At the extremes, either a line encircles infinity or it encircles a point, the ultimate finity. Since finity and infinity are (by definition) absolute opposites, they ensure that our straight line and our curved line are also absolute opposites (in a related sense).

Thus we conclude that our most asymmetrical spiral must incorporate two components, one that approaches a straight line and one that approaches a circular point. The Pi relationship between a radial line and its circle expresses the same intensity of contrast as Spencer-Brown's mark of distinction, which is one reason why it has always been compared to (and in our time named after) the transcendental.

As it happens, there is one extremely elegant spiral that fits our prescription. The reciprocal or hyperbolic spiral, r= 1, consists of a continuous transition between circling ever-closer to the origin (the ultimate infinitesimal finity) and extending along the line y = 1 as r approaches infinity. The reciprocal spiral most elegantly models the transition from circle to line, from the infinitesimal finity to the infinite. It is nowhere self-similar in any way. Thus it is the perfect complement to the symmetry of the tetrahedron (when it is drawn out into a full vortex on the surface of a dimpled-sphere torus, as described elsewhere. The specially shaped, 1 1/2-turn spiral vortex can be understood to have components that are complementary to those of the tetrahedron. Where the tetrahedron has 7-radial axes of spin symmetry, the spiral vortex on a torus can be defined by 7-distinct cyclic regions arrayed in sequence. The 7-radial axes are complementary to the 7-cyclic regions.)

While different conventions for modeling symmetry and asymmetry would likely produce different forms, given our choice of a tetrahedral frame to model symmetry in 3-dimensional space, the reciprocal spiral (projected in 3-dimensions on a spherical torus) may be its best asymmetrical complement. Together they represent one way to model the primary distinction between symmetry and asymmetry and Spencer-Brown's topologically fundamental and primary distinction between inside and outside.