Sculpture ©1996 S. Tenen & J. Fournier
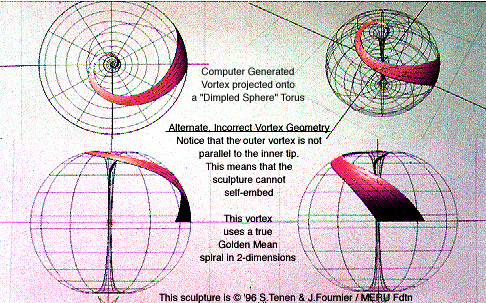
This 3-dimensional vortex sculpture (whose design is discussed on our unreleased videotape, ©1988) is an example of how not to solve a problem. This spiral vortex looks good, but it is meaningless. The Golden Mean is an important proportion – and that suggested that we should examine the Golden Mean spiral, which exhibits some properties of the Golden Mean proportion, as a candidate spiral component for our vortex sculpture. But the Golden Mean spiral (shown above, upper left) and the Golden Mean pseudo-spiral (which looks almost the same, but is a geometric approximation and not a true algebraic spiral), like all logarithmic spirals, is self-similar. No matter where you examine it, it always has the same shape at any and all orientations. In 2-dimensions, these spirals self-embed because they are self-similar. (Note: The Golden Mean spiral, a true logarithmic spiral, is often confused with a Fibonacci spiral by uneducated occultists. There are, in fact, an infinite number of spirals, based on the Fibonacci numbers, that are NOT Golden Mean spirals. Most ordinarily constructed Fibonacci spirals are also logarithmic spirals.*)
However, when a logarithmic spiral (such as the Golden Mean spiral) is projected onto a sphere (not shown) or onto a Dimpled-Sphere (as shown above), it cannot self-embed. This is because the outer part of the vortex is not and can not be parallel to the inner tip. Thus, if one of these Dimpled-Sphere vortices were to be embedded in another (at the tip, like a seed-pit in a fruit), it would not fit. The ends of the vortex-spirals could not line up.
- To put one of these vortices inside another would be like forcing a square peg into a round hole.
Since the sculpture we were seeking to design was intended to model (among other important properties) the philosophical recursion of life, generation after generation, "fruit tree yielding fruit whose seed is inside itself" (Genesis 1:11), by means of self-embedment, it was necessary for us to either mechanically modify the logarithmic or Golden Mean spiral, or to replace it with another form. As far as the usefulness and esthetics of our sculpture are concerned, it does not matter how we accomplish this. Philosophically, it would be pleasing to find a single elegant function (or a simple assembly of simple functions) that would have the correct shape, but for visual and esthetic purposes it is just as proper to merely bend the vortex until the outer end is parallel to the inner tip. Within our ability to see, the "hand-made" vortex adjusted to be esthetically pleasing would be indistinguishable from the generated form.
We know of three sets of specially arranged algebraic functions and at least one geometric construction that produces Meru Foundation’s FIRST HAND "Flame-letter" vortex sculptures. All of these appear identical and all self-embed because their outer ends and their inner tips are parallel. Even though these spiral vortices self-embed, they are not self-similar. In fact, if they were, that would also disqualify them for our purposes.
This is because we are attempting to model the contrast between symmetry and asymmetry, with symmetry represented by a tetrahedron and asymmetry represented by a spiral vortex. The self-similiar logarithmic, Golden Mean, spirals are simply too symmetrical. That is what self-similar means. The MERU FIRST HAND "Flame Letter" sculpture makes use of the most Asymmetric spiral (and the spiral vortex that comes from it) so that it will be a proper complement to our choice of an entirely symmetrical (compact, and elegant) tetrahedron to represent symmetry. (See The Light in the Meeting Tent in the Archives section on our Internet Website.)
It should be noted that the sample Golden Mean spirals above have been deliberately projected onto Dimpled-Sphere tori with smaller (and narrower) than optimum holes. There are two reasons for this: 1. It makes the tip and end angles more distinct and easy to see, and 2. Because the "dimples" are small and narrow, the Dimpled-Sphere and the vortex on it are identical to an ordinary sphere for most of the outside of the vortex. This makes it easier to see that the shape and angles of the vortex on an ordinary sphere would be the same as on our Dimpled-Sphere without the need for another drawing. When the hole is wider, the spiral twists deeper in it. When the hole is narrow, as shown, the spiral twist is nearer to the top. Otherwise all logarithmic spirals take the same form. No matter how we change the shape of the Dimpled-Sphere, the vortex sculpture never self-embeds. If we stretch the Dimpled-Sphere into a more elongated shape, the outer end appears to straighten somewhat, but it still can never be parallel to the inner tip and, consequently, it cannot self-embed.
It should also be noted that for the limited purpose of making alphabetic letter shapes alone, any spiral vortex, based on almost any common spiral, would work, including even the non-recursive vortices based on logarithmic spirals - and the spiral vortex does not even have to be fitted to the surface of a Dimpled-Sphere torus or trimmed to 1-1/2 turns in order to do so.
- Even a randomly coiled wire coat-hanger is capable of generating all of the letter shapes of most alphabets. But this means nothing and proves nothing.
But, we are not searching for a alphabet letter shape generator alone; we are attempting to design a philosophically meaningful form that represents the important aspects of a wide range of philosophical, religious, cultural and scientific paradigms. No special sculpture is needed to make alphabetic letters. (We will eventually post a range of alternate sculptural forms capable of generating various alphabetic letters on our Internet Website.)
A very special sculpture is required to model the philosophical
principles
that we chose to include. That is why a model human Hand based on
specially
shaped Torus Knots that model mathematical Singularities is meaningful,
while a randomly or inappropriately defined vortex - even one that
superficially
appears similar to ours (like the logarithmic spiral vortex illustrated
above) - is not meaningful.
********************************************************
(For Dr. Stewart's complete letter, see http://www.newscientist.com/article.ns?id=mg18725180.400)
Regarding the term “Golden Mean”, the following is from The Mathematics of Plato’s Academy, ©1987 D.H. Fowler. Clarendon Press: Oxford Science Publications, Oxford UK.ISBN 0-19-853947-9, p. 105, in the notes and references to Ch. 3, The Dimension of Squares:
Contents of this page are ©1996 Stan Tenen,
and licensed to Meru Foundation, 524 San Anselmo Ave. #214, San Anselmo, CA 94960.
Email inquiries to: meru@meru.org